Построение серединного перпендикуляра с помощью циркуля

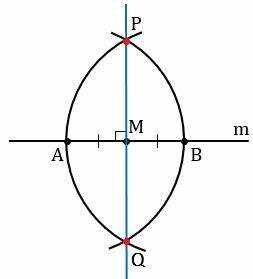
Серединный перпендикуляр является важным конструктивным элементом в геометрии, применяемом для решения различных задач. Он позволяет находить среднюю точку отрезка и обеспечивает перпендикулярное направление, что особенно полезно при построении фигур и решения геометрических проблем. В этой статье мы рассмотрим, как построить серединный перпендикуляр к отрезку с помощью циркуля и линейки, используя простые и понятные шаги.

Построение серединного перпендикуляра – это процесс, который требует внимательности и точности. Основной принцип заключается в том, чтобы сделать два одинаковых окружности с центрами в концах отрезка. Точки пересечения этих окружностей образуют направление перпендикуляра. Важно понимать, что правильное выполнение всех этапов гарантирует высокий уровень точности в построении.

Основы работы с циркулем

При работе с циркулем важно соблюдать несколько простых правил. Во-первых, держите циркуль уверенно, чтобы избежать смещения во время рисования. Во-вторых, выбирайте правильный радиус: он должен быть удобным для работы и соответствовать задачам, которые необходимо решить.

Чтобы начать строить фигуры, сначала установите одну ножку циркуля в точку, а другой — взяв за нужный радиус, нарисуйте круг. Это позволяет точно копировать расстояние, создавая необходимые фигуры. Также циркуль часто используется для нахождения точек пересечения окружностей, что является основой для более сложных построений.

Знание основ работы с циркулем поможет не только в учебе, но и в практических задачах. Например, рисунок гусь лапчатый это можно выполнить с использованием циркуля для точного определения необходимых размеров.

Определение серединного перпендикуляра

Основные характеристики серединного перпендикуляра включают:

• Находится на равном расстоянии от концов отрезка.
• Пересекает отрезок под прямым углом.
• Любая точка на серединном перпендикуляре равновелико удалена от концов отрезка.

Серединный перпендикуляр играет важную роль в различных геометрических конструкциях и доказательствах.

Например, в треугольниках, серединные перпендикуляры сторон используются для нахождения центра окружности, которая описана вокруг треугольника.

Понимание серединного перпендикуляра является основой для дальнейших изучений в плоскостной геометрии и прикладных задачах, таких как построение фигур и решение треугольников.

Необходимые инструменты для работы

Для построения серединного перпендикуляра циркулем потребуется минимальный набор инструментов, который обеспечит точность и удобство в работе. Вот список необходимых предметов:

• Циркуль: основной инструмент для выполнения построений. Убедитесь, что он в хорошем состоянии и острые концовки обеспечивают четкое нанесение окружностей.
• Линейка: потребуется для измерения и проведения линий. Лучше всего использовать прозрачную линейку, чтобы видеть, где именно вы проводите линии.
• Карандаш: выберите карандаш с тонким грифелем для точного нанесения отметок, которые не будут мешать построению.
• Бумага: идеальным вариантом будет гладкая бумага, на которой легко провести линии и отметить важные точки.
• Транспортир: может понадобиться для проверки углов, особенно если вы хотите убедиться, что перпендикуляр действительно 90 градусов.

Наличие этих инструментов поможет вам успешно выполнить построение серединного перпендикуляра с максимальной точностью и легкостью.

Как выбрать правильный циркуль

Тип циркуля. Существуют различные виды циркулей: стандартные, мини-циркули, циркули с фиксатором и профессиональные модели. Для школьной программы обычно достаточно стандартного циркуля, в то время как для профессионального использования лучше выбирать специализированные инструменты.

Материалы. Циркули изготавливаются из различных материалов, включая металл и пластик. Металлические циркули более долговечны и обеспечивают лучшую точность, тогда как пластиковые модели часто легче и дешевле.

Диаметры и механизмы. Убедитесь, что расстоянние между концами циркуля регулируется плавно и надежно фиксируется. Большинство моделей имеют возможность установить нужный радиус, что облегчает процесс работы. Проверьте диапазон, на который способен циркуль, особенно если вы планируете работать с большими фигурами.

Удобство в использовании. Проверьте, насколько удобно держать циркуль в руках. Рукоятки должны быть удобными, а острия – достаточно острыми для четкого нанесения меток. Это важно для точной работы и минимизации усилий.

Цена. Стоимость циркуля может варьироваться. Важно найти баланс между ценой и качеством. Не всегда дорогой инструмент означает лучшее выполнение задач; иногда существуют вполне доступные варианты, которые выполнять свою функцию на высоком уровне.

Выбирая циркуль, учитывайте свои потребности и уровень навыков. Таким образом, вы сможете обеспечить себе инструмент, который будет надежным помощником в вашей учебе или профессиональной деятельности.

Подготовка линии для измерений

Перед тем как приступить к построению серединного перпендикуляра с помощью циркуля, важно правильно подготовить линию для измерений. Это обеспечит точность и правильность ваших действий.

1. Выбор подходящей линии:
   • Убедитесь, что линия, по которой вы будете работать, является прямой и четко видимой.
   • Используйте максимальную длину линии, чтобы упростить процесс измерения.
2. Очистка рабочей поверхности:
   • Удалите все препятствия, такие как мел, карандаш или другие материалы, которые могут скрывать линию.
   • Обязательно проверьте, чтобы на поверхности не было пыли или мусора.
3. Нанесение исходной линии:
   • Используйте линейку для того, чтобы провести ровную линию с помощью карандаша.
   • При необходимости используйте угольник для проверки правильного угла.
4. Разметка точек:
   • Выделите точки, которые будут служить опорными для построения серединного перпендикуляра.
   • Подсчитайте количество отрезков, если это необходимо, например, что значит кратное трем в контексте ваших измерений.

Следуя этим шагам, вы создадите оптимальную основу для дальнейших действий по построению серединного перпендикуляра.

Построение окружностей: основные шаги

Шаг 1: Установите циркуль на точке, где хотите, чтобы находился центр окружности. Это может быть любая произвольная точка на чертеже.

Шаг 2: Определите радиус окружности. Для этого установите одну из ножек циркуля на центр, а другую – на расстоянии, равном радиусу. Подождите, пока циркуль будет стабилен.

Шаг 3: Вращайте циркуль вокруг центра, не двигая первую ножку, чтобы описать окружность. Убедитесь, что линия окружности плавная и равномерная.

Шаг 4: Если необходимо, повторите процесс с другим центром и радиусом. Cela позволит создать несколько окружностей, пересекающихся или расположенных рядом друг с другом.

Формирование окружностей требует практики, чтобы достичь идеального результата. Также это связано с навыками работы с геометрическими инструментами.

При проектировании окружностей полезно помнить о том, что точность может повлиять на итоговые результаты работы. Используйте правильные инструменты и соблюдайте все шаги аккуратно.

Дополнительные знания о социальных отношениях можно найти у каких людей возникли социальные отношения, что также помогает лучше понять контекст работы с инструментами.

Нахождение точек пересечения окружностей

Для нахождения точек пересечения двух окружностей необходимо использовать свойства геометрии. Будем считать, что у нас есть две окружности с центрами в точках A и B, и радиусами R1 и R2 соответственно.

Процесс можно разделить на несколько этапов:

1. Определите расстояние между центрами окружностей A и B. Это расстояние обозначим как d.

2. Условие пересечения окружностей. Они будут пересекаться, если выполняются следующие условия:

• d < R1 + R2 (окружности пересекаются);
• d > |R1 — R2| (одна окружность не содержится внутри другой).

3. Если окружности не пересекаются, дальнейшие действия не требуются. Если же они пересекаются, перейдите к следующему этапу.

4. Построение прямой, соединяющей центры A и B. Эта прямая будет проходить через точки пересечения окружностей или делить расстояние между ними.

5. На этой прямой отметьте отрезок, равный R1 и R2, от центра каждой окружности. Это означает, что вам нужно провести перпендикуляры на заданной длине от центра A и B. Перпендикуляры будут пересекаться в точках, которые являются искомыми точками пересечения окружностей.

6. Получившиеся точки пересечения — это искомые точки, которые можно использовать для дальнейших построений или расчетов.

Как провести серединный перпендикуляр

Чтобы провести серединный перпендикуляр к отрезку, начните с нанесения на него маркировок. Определите две специальные точки на отрезке, между которыми будет проводиться перпендикуляр. Эти точки могут быть любыми, но часто выбираются с учетом удобства последующих измерений.

Следующим шагом является установка циркуля в одну из выбранных точек. Расстояние между острием циркуля и второй точкой отрезка должно быть более половины длины отрезка, чтобы окружности пересекались.

После этого нарисуйте первую окружность. Не убирая циркуля, переместите его к другой точке и также нарисуйте вторую окружность. Эти две окружности должны пересекаться в двух точках.

Теперь аккуратно соедините точки пересечения окружностей прямой линией. Эта линия и будет серединным перпендикуляром к изначальному отрезку.

Для точности рекомендуется повторить процесс несколько раз и сравнить полученные результаты. Это поможет избежать ошибок и достичь более точного результата.

Проверка точности построения

После выполнения всех шагов по построению серединного перпендикуляра важно убедиться в его точности. Существует несколько способов проверить правильность конструкции.

Первый метод проверки заключается в использовании линейки: измерьте расстояние от точек пересечения серединного перпендикуляра до концов отрезка. Если расстояния равны, построение выполнено корректно.

Кроме того, вы можете воспользоваться циркулем. Для этого установите его одну ногу в точку пересечения и правую ногу поместите в одну из сторон отрезка. Затем отметьте точку. Повторите ту же операцию с другой стороны отрезка. Если обе точки совпадают, конструкция верна.

Для более наглядной проверки можно воспользоваться таблицей, в которой будут записаны результаты измерений:

Измерение	Результат 1	Результат 2
Расстояние до точки A	[значение]	[значение]
Расстояние до точки B	[значение]	[значение]

Сравните значения, и если они совпадают, это подтверждает, что серединный перпендикуляр построен точно. Небольшие погрешности могут возникать из-за человеческого фактора или несовершенства инструментов, поэтому стоит уделять внимание аккуратности и точности всех измерений.

Ошибки при построении и их решение

Еще одной частой ошибкой является неверное положение циркуля при проведении окружностей. Если циркуль не удерживается строго вертикально, окружности могут быть искажены, что затруднит нахождение точек пересечения. Решением будет постоянная проверка положения циркуля и его устойчивое удержание во время рисования окружностей.

Также стоит обратить внимание на точность определения точек пересечения окружностей. Часто их можно не увидеть из-за небольшого радиуса или недостаточной четкости линий. В таких случаях стоит использовать острый карандаш и рисовать окружности с большей четкостью, а также проверять расположение с помощью линейки.

Наконец, ошибки могут возникнуть на этапе построения перпендикуляра. Если линии, соединяющие точки пересечения, проведены неаккуратно, могут возникнуть неверные углы. Для избегания данной ошибки рекомендуется использовать линейку и транспортир для более точного проведения линий, что поможет получить четкие и правильные углы.

Практические примеры использования метода

Метод построения серединного перпендикуляра циркулем находит полезное применение в различных областях, начиная от школьного обучения и заканчивая профессиональной инженерией и архитектурой.

В школьном курсе математики этот метод часто используется для решения задач на построение фигур. Например, нахождение центра окружности, построенной по заданным концам отрезка, позволяет учащимся лучше понять свойства фигур и их взаимосвязь.

В архитектуре серединный перпендикуляр помогает определить правильное расположение стен и структурных элементов. Это важно для обеспечения устойчивости построек и их дальнейшей эксплуатации.

Инженеры применяют этот метод при проектировании различных конструкций, таких как мосты или каркасные здания. Определение центра тяжести элементов также можно выполнить с помощью построения серединного перпендикуляра.

Кроме того, в геометрии и топографии метод используется для построения биссектрис, что упрощает задачи по делению углов и нахождению равновесных точек между разными линиями или объектами.

Практическое применение метода серединного перпендикуляра расширяется до различных естественных наук, где требуется точность в измерениях и построениях. Например, в физике для нахождения точек приложения сил или центров масс тел.

Таким образом, метод построения серединного перпендикуляра с использованием циркуля является универсальным инструментом, который находит применение в самых разных областях знаний и профессиях.

Влияние масштаба на точность

При работе в большом масштабе (например, на больших листах бумаги) ошибки, возникающие при измерениях, могут быть менее заметными, однако они все равно существуют и могут накапливаться, особенно при выполнении нескольких последовательных операций. В маленьком масштабе (например, при работе на миллиметровой бумаге) каждая ошибка становится более ощутимой и может привести к заметным погрешностям.

Кроме того, свойства самого циркуля и его размеры также влияют на точность построений. Циркуль с большим радиусом может создать большее количество ошибок, необходимых для точного нахождения пересечений окружностей.

Масштаб	Влияние на точность
Малый	Увеличивает значимость мелких ошибок
Средний	Некоторые ошибки становятся менее заметными
Большой	Ошибки могут скрываться, но накапливаться

Оптимальный выбор масштаба позволяет минимизировать ошибки, что в свою очередь гарантирует более точное построение серединного перпендикуляра. Основное внимание следует уделить выбору правильного масштаба в зависимости от задач, которые вы перед собой ставите.

Разнообразие применения серединного перпендикуляра

Серединный перпендикуляр занимает важное место в геометрии и различных областях науки и техники. Этот простой, но эффективный инструмент применяется в самых различных задачах, от теоретических до практических.

Архитектура и строительство: в архитектурном проектировании серединный перпендикуляр используется для создания ровных и гармоничных планов зданий. Он позволяет точно определять расположение стен, перегородок и других элементов конструкции, что способствует более качественному процессу проектирования.

Топография: при создании топографических карт и планов территории, серединные перпендикуляры помогают в точной нивелировке и определении высотных отметок. Этот метод позволяет быстро и эффективно находить центральные оси объектов.

Машиностроение: в машиностроении, серединные перпендикуляры применяются при разработке деталей и узлов механизмов. Это необходимо для обеспечения точности сборки и функционирования механизмов, где важна симметрия и равновесие.

Образование: в учебном процессе серединный перпендикуляр служит основным инструментом для обучения геометрическим основам. Он помогает развивать пространственное мышление и навыки черчения, что является важной частью математического образования.

Дизайн и рисование: в графическом дизайне и художественном творчестве применение серединного перпендикуляра помогает в создании пропорциональных и симметричных композиций. Он способствует более точному размещению элементов и улучшению визуального восприятия.

Научные исследования: в научной практике серединные перпендикуляры могут использоваться для анализа структур данных, моделирования и проведения экспериментов, связанных с анализом формы и симметрии объектов.

Таким образом, разнообразие применения серединного перпендикуляра является обширным и охватывает множество сфер деятельности, где требуется высокая точность и аккуратность в измерениях и построениях.