Преобразование чисел между различными системами счисления является важным навыком в математике и информатике. Шестнадцатеричная система, также известная как система счисления с основанием 16, широко используется в программировании, компьютерной графике и других областях. В этой статье мы рассмотрим, как преобразовать число 19 в шестнадцатеричную систему.
Сначала необходимо понять, как работает шестнадцатеричная система. В этой системе используются 16 символов: от 0 до 9 и от A до F, где буквы A, B, C, D, E и F представляют числа от 10 до 15 соответственно. Таким образом, каждое шестнадцатеричное число соответствует своему значению в десятичной системе.
Чтобы выполнить преобразование, мы будем делить число 19 на 16 и отслеживать остатки. Результаты деления и остатки как раз и образуют шестнадцатеричное представление. В результате, мы получим, что 19 в шестнадцатеричной системе будет представлено как 13.
Основы систем счисления
Системы счисления представляют собой способ представления чисел с использованием определенного набора символов. Наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы. Каждая из этих систем основана на своих уникальных основаниях, что влияет на количество возможных символов, используемых для записи чисел.
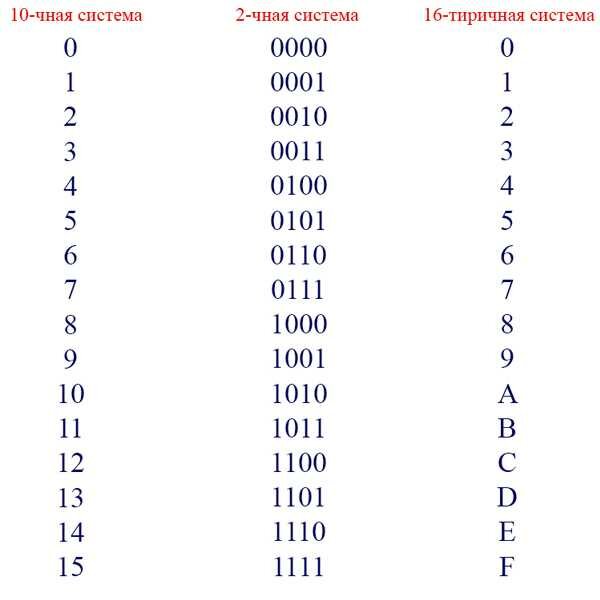
В десятичной системе, основание которой равно 10, используются символы от 0 до 9. В двоичной системе, основание 2, представление чисел ограничивается всего двумя символами: 0 и 1. Восьмеричная система, основание 8, использует символы от 0 до 7, а шестнадцатеричная система, основание 16, включает символы от 0 до 9 и дополнительные буквы от A до F, которые представляют числа от 10 до 15.
| Система счисления | Основание | Символы |
|---|---|---|
| Десятичная | 10 | 0-9 |
| Двоичная | 2 | 0, 1 |
| Восьмеричная | 8 | 0-7 |
| Шестнадцатеричная | 16 | 0-9, A-F |
Понимание основ систем счисления позволяет легко преобразовывать числа из одной системы в другую, что имеет важное значение в различных областях, таких как программирование, электронные вычисления и цифровая обработка сигналов.
Шестнадцатеричное представление чисел
Шестнадцатеричная система счисления, также известная как шестнадцатеричная, базируется на числе 16 и использует 16 символов для представления чисел: 0-9 и A-F. В этой системе цифры от 0 до 9 представляют собой значения от нуля до девяти, тогда как буквы от A до F обозначают значения от десяти до пятнадцати соответственно.
Шестнадцатеричная запись широко используется в информатике, особенно для упрощения работы с бинарными данными. Один шестнадцатеричный символ соответствует четырем двоичным битам, что делает необходимым количество разрядов значительно меньше при представлении больших чисел.
Например, число 19 в десятичной системе преобразуется в шестнадцатеричное представление 13, что можно легко вычислить, деля 19 на 16 и округляя до ближайшего целого. Оставшаяся часть после деления также переводится в шестнадцатеричное значение.
Применение шестнадцатеричной системы не ограничивается только программированием. Она также находит применение в различных областях, включая дизайн графики и компьютерные сети. В веб-разработке часто используется для обозначения цвета, что позволяет легко интерпретировать и передавать цветовые данные.
Таким образом, понимание и использование шестнадцатеричной системы счисления поможет лучше ориентироваться в мире технологий и информационных систем. Дополнительную информацию о цифровых представлениях можно найти, например, в контексте симуляций, связанных с рынком специй симс 4 где.
Преобразование из десятичной системы
Преобразование чисел из десятичной системы в другие системы счисления, такие как шестнадцатеричная, осуществляется через деление на основание целевой системы. В случае с шестнадцатеричной системой основание равно 16. Метод преобразования включает последовательные деления числа на 16 с записью остатков от деления.
При делении десятичного числа 19 на 16 получается целая часть 1 и остаток 3. Это значит, что 19 в шестнадцатеричной системе будет представлено как 13, где 1 – это коэффициент десятков (16?), а 3 – единицы (16?). Записывая эти значения, мы получаем число 13.
Таким образом, процесс включает в себя деление, нахождение остатков и, в конечном итоге, составление шестнадцатеричного представления из полученных значений. Этот метод будет работать для любого десятичного числа, что позволяет легко и быстро преобразовывать числа в нужную систему счисления.
Алгоритм перевода числа 19
Для преобразования десятичного числа 19 в шестнадцатеричную систему счисления, можно использовать метод деления на основание системы с последующим получением остатков.
Пошаговый алгоритм выглядит следующим образом:
- Начинаем с числа 19. Делим его на 16 (основание шестнадцатеричной системы). Получаем частное 1 и остаток 3.
- Записываем остаток, который соответствует шестнадцатеричному значению 3.
- Теперь берем частное 1 и делим его на 16. Получаем частное 0 и остаток 1.
- Записываем остаток, который соответствует шестнадцатеричному значению 1.
Теперь мы берем все полученные остатки и записываем их в обратном порядке: 1 и 3. Таким образом, число 19 в шестнадцатеричной системе представляется как 13.
Для более подробной информации о других открытиях в области систем счисления, вы можете посетить берег какой бывает.
Цифры шестнадцатеричной системы
Шестнадцатеричная система счисления, также известная как базовая 16, использует для представления чисел 16 уникальных символов: цифры от 0 до 9 и буквы от A до F. В этой системе буквы соответствуют числам от 10 до 15, где A обозначает 10, B – 11, C – 12, D – 13, E – 14 и F – 15.
Шестнадцатеричная система широко используется в вычислительной технике и программировании, так как она позволяет компактно представлять большие числа. Преобразование из двоичной в шестнадцатеричную систему значительно облегчает работу с двоичными данными, так как каждая шестнадцатеричная цифра соответствует четырем двоичным битам.
Кроме того, шестнадцатеричная система упрощает отображение значений, таких как цветовые коды в веб-дизайне. Например, цвет RGB можно выразить как комбинацию трех шестнадцатеричных значений: два для красного, два для зеленого и два для синего компонентов.
Таким образом, благодаря удобству и компактности, шестнадцатеричная система занимает важное место в современном программировании и информационных технологиях. Для более глубокого понимания этой темы можно ознакомиться с анастасия падежи.
Каковы символы от 0 до F
- 0 — ноль
- 1 — один
- 2 — два
- 3 — три
- 4 — четыре
- 5 — пять
- 6 — шесть
- 7 — семь
- 8 — восемь
- 9 — девять
- A — десять
- B — одиннадцать
- C — двенадцать
- D — тринадцать
- E — четырнадцать
- F — пятнадцать
Каждый символ в этом наборе представляет собой определенное значение, где цифры от 0 до 9 соответствуют своим обычным значениям, а буквы A-F представляют значения от 10 до 15. Таким образом, шестнадцатеричная система позволяет кратко записывать числа, используя всего 16 символов.
Разбиение числа на части
Для успешного преобразования числа 19 в шестнадцатеричную систему необходимо внимательно рассмотреть его составные элементы. Разбиение числа на части помогает понять, как каждая из составляющих влияет на конечный результат. В данном случае число 19 может быть представлено как сумма различных степеней двойки.
В десятичной системе оно равно 1*10^1 + 9*10^0. Однако для шестнадцатеричного представления удобно разбить число на целые и дробные компоненты, если таковые имеются.
В нашем случае число 19 не имеет дробной части. Для разбиения на части мы можем анализировать его как сумму восьмёрок и единиц:
| Часть | Значение |
|---|---|
| 16 | 1 |
| 3 | 3 |
Таким образом, 19 можно представить как 16 (что соответствует первой цифре в шестнадцатеричной системе) и 3 (вторая цифра). Это выражение в шестнадцатеричной системе будет записано как 13. Разбиение на части позволяет чётко увидеть, как число 19 трансформируется и соответствует определённым символам в другой системе счисления.
Работа с остатками при делении

Преобразование чисел из одной системы счисления в другую требует использования деления с остатку. Этот процесс позволяет находить значения, которые необходимо использовать в системе счисления, куда мы переводим число.
При делении числа 19 на основание целевой системы (в нашем случае на 16) мы получаем целую часть и остаток. Остаток представляет собой ту цифру, которая будет соответствовать младшему разряду в шестнадцатеричной системе. Процесс деления продолжается до тех пор, пока целая часть не станет равной нулю.
Каждый полученный остаток следует запоминать, поскольку он будет образовывать итоговое число в обратном порядке. Таким образом, работа с остатками является ключевым элементом в процессе преобразования, так как именно они определяют цифры, вошедшие в итоговое представление числа.
Например, в случае с числом 19, при делении на 16, целая часть равна 1, а остаток равен 3. При повторном делении (уже числа 1) на 16, целая часть будет 0, остаток равен 1. Полученные остатки 1 и 3 составляют число в шести значениях: 13 в шестнадцатеричной системе представляется как 13.
Использование остатка при делении помогает нам понять структуру чисел в разных системах и важность каждого разряда, что критично для правильного перевода и интерпретации чисел.
Примеры перевода чисел
Перевод чисел в шестнадцатеричную систему может быть полезен в различных областях, включая программирование и цифровую электронику. Рассмотрим несколько примеров, чтобы лучше понять процесс преобразования.
Пример 1: Рассмотрим число 15. При делении на 16, мы получаем 0 с остатком 15. В шестнадцатеричной системе число 15 представляется как F.
Пример 2: Число 255. Делим 255 на 16, получаем 15 (целая часть) и остаток 15. Целая часть 15 в шестнадцатеричном представлении – это также F. Таким образом, 255 в шестнадцатеричной системе будет FF.
Пример 3: Теперь возьмем число 4095. Делим на 16: 4095 / 16 = 255 с остатком 15. Затем делим 255 на 16: 255 / 16 = 15 с остатком 15. Наконец, 15 делим на 16: 15 / 16 = 0 с остатком 15. Таким образом, 4095 в шестнадцатеричной системе представляется как FFF.
Пример 4: Посмотрим на число 32. Делим 32 на 16: 32 / 16 = 2 с остатком 0. Поэтому в шестнадцатеричной системе 32 будет 20.
Эти примеры показывают, как можно преобразовывать разные числа в шестнадцатеричную систему, используя алгоритм деления и остатка, что делает процесс более понятным и доступным.
Сравнение десятичного и шестнадцатеричного
Десятичная и шестнадцатеричная системы счисления существенно различаются в своих принципах представления чисел и используются в разных контекстах. Рассмотрим их основные отличия и сходства.
Основные характеристики
- Основание системы: Десятичная система имеет основание 10, что означает использование десяти уникальных цифр (0-9). Шестнадцатеричная система имеет основание 16 и включает шестнадцать символов (0-9 и A-F).
- Представление чисел: В десятичной системе каждое положение числа соответствует степени десяти, тогда как в шестнадцатеричной – степени шестнадцати.
- Число символов: Шестнадцатеричная система использует больше символов для представления тех же чисел, что позволяет более компактно записывать большие значения.
Использование в практике
- Десятичная система: Применяется в повседневной жизни, бухгалтерии, а также в большинстве научных расчетов.
- Шестнадцатеричная система: Широко используется в компьютерных науках, программировании, а также для обозначения цветов в веб-дизайне.
Преимущества и недостатки
-
Десятичная система:
- Преимущество: Интуитивность и привычность для большинства людей.
- Недостаток: Более длинное представление больших чисел по сравнению с шестнадцатеричной.
-
Шестнадцатеричная система:
- Преимущество: Компактность записи больших чисел.
- Недостаток: Может быть сложнее воспринимается для новичков без предварительной подготовки.
Сравнение этих систем позволяет лучше понять, в каких ситуациях и почему используется каждая из них, а также помогает в процессе преобразования чисел между системами счисления.
Использование калькуляторов для перевода
При использовании калькулятора для перевода числа 19 в шестнадцатеричную систему достаточно ввести число в десятичной системе и выбрать соответствующую функцию преобразования. Большинство калькуляторов автоматически отображает результат, что позволяет экономить время и минимизировать вероятность ошибок, которые могут возникнуть при ручном подсчете.
Такой способ перевода особенно удобен для студентов, инженеров и программистов, которым часто требуется работать с различными системами счисления. Однако важно понимать, что знание алгоритма перевода и основ систем счисления также полезно, так как это способствует глубокому пониманию темы и улучшает математическую грамотность.
В некоторых случаях, калькуляторы могут работать по принципу, который описывает процесс преобразования, позволяя пользователю видеть промежуточные шаги. Это помогает закрепить понимание логики преобразования чисел и развивает навыки работы с различными системами счисления.
Программное обеспечение для преобразований
Существуют различные программные инструменты, которые помогут выполнить преобразование чисел между системами счисления. Чаще всего они представлены в виде онлайн-калькуляторов, настольных приложений и библиотек для программирования.
Онлайн-калькуляторы достаточно просты в использовании: просто вводите число в десятичной системе, и средство мгновенно показывает его эквивалент в шестнадцатеричной системе. Такие инструменты особенно полезны для быстрого выполнения расчетов без необходимости установки дополнительного ПО.
Настольные приложения могут предложить больше функций, таких как возможность работы с большими числами, сохранение истории расчетов или поддержка других систем счисления, таких как двоичная или восьмеричная. Программное обеспечение для математики и инженерных расчетов, например, MATLAB или Mathematica, также поддерживает подобные преобразования через встроенные функции.
Для программистов существуют библиотеки, позволяющие выполнять подобные преобразования в рамках кодирования. Например, в языках программирования, таких как Python, Java или C++, часто доступны встроенные функции для выполнения конверсий между различными системами счисления, что позволяет интегрировать преобразования в более сложные алгоритмы.
Таким образом, использование программного обеспечения для преобразований значительно упрощает процесс работы с числами и позволяет избежать ошибок, которые могут возникнуть при вручном подсчете.
Примеры в реальной жизни
Шестнадцатеричная система имеет широкое применение в различных областях. Например, веб-разработка активно использует шестнадцатеричные коды для задания цветов в CSS. Каждый цвет описывается шестизначным кодом, где первые две цифры представляют красный, следующие две – зеленый, а последние две – синий компоненты цвета.
В программировании и низкоуровневой разработке шестнадцатеричные значения часто используются для представления адресов памяти и данных. Это позволяет более наглядно работать с байтами и их группами, особенно при отладке кода.
В электротехнике и цифровых системах, большинство микроконтроллеров и процессоров используют шестнадцатеричные значения для представления настроек, конфигураций и регистров. Это упрощает чтение данных и взаимодействие с устройствами.
Во время работы с базами данных, шестнадцатеричные значения также могут использоваться для кодирования бинарных данных, что позволяет существенно экономить место и облегчает хранение.
Таким образом, преобразование чисел из десятичной системы в шестнадцатеричную не только важно в теории, но и находит множество практических приложений в реальном мире.
Где применяются шестнадцатеричные числа
Шестнадцатеричная система чисел находит широкое применение в различных областях, связанных с вычислительными технологиями и цифровыми системами. Она особенно полезна для упрощения представления бинарных данных, так как один шестнадцатеричный символ соответствует четыре битам.
Одной из основных сфер применения шестнадцатеричных чисел является программирование. Многие языки программирования используют шестнадцатеричное представление для задания значений переменных, адресов в памяти и для работы с цветами в веб-дизайне. Например, цвет в формате RGB может быть представлен в шестнадцатеричном виде (например, #FF5733), что делает код более компактным и читабельным.
Кроме того, шестнадцатеричные числа широко используются в системах управления памятью и в машинном коде, где важно представлять значения в удобочитаемой форме. Это особенно актуально для отладки программ и анализа производительности, когда разработчики работают с двоичных данных и удаляют лишние сложности.
Шестнадцатеричные значения также применяются в сетевых протоколах и IP-адресации, где использование более коротких представлений помогает экономить место и время при передаче данных. Бывает также полезно представлять коды символов в шифрах и системах кодирования, таких как UTF-8.
В дополнение к этим областям, шестнадцатеричные числа активно используются в научных вычислениях как способ представления сложных чисел и форматирования данных для графиков и таблиц, что позволяет визуализировать результаты более наглядно.
Ошибки в переводе чисел

Перевод чисел между системами счисления может быть сложной задачей, особенно если не учитывать некоторые распространенные ошибки. Ниже представлены основные типы ошибок, которые могут возникнуть при переводе десятичного числа 19 в шестнадцатеричную систему.
- Ошибки в делении: Путаница в процессе деления может привести к неправильным остаткам. Необходимо тщательно следить за шагами алгоритма, чтобы избежать потери значений.
- Неправильное использование числовых систем: Иногда можно ошибиться, применяя правила одной системы к другой. Например, путать диапазоны цифр в десятичной и шестнадцатеричной системах.
- Неучтённые остатки: Пропуск остатков в промежуточных вычислениях приводит к неверному представлению числа. Важно фиксировать каждый этап процесса.
Следует также отметить, что при работе с шестнадцатеричными числами можно столкнуться с путаницей из-за дополнительных символов (например, A-F), что добавляет уровень сложности.
Распространенные ошибки в расчетах
- Неправильное деление на 16: Например, деление 19 на 16 может быть ошибочно выполнено как целочисленное деление.
- Сложности с переводом остатков: Иногда остаток может быть неправильно интерпретирован или не записан в нужном виде.
- Игнорирование порядка записи: Порядок, в котором записываются цифры результата, очень важен. Ошибки в последовательности могут навести на неверный итог.
Важно перед началом работы проговорить алгоритм в черновиках и проверить все промежуточные результаты, чтобы избежать вышеописанных ошибок. Уделив внимание каждому этапу, можно значительно снизить вероятность ошибок в переводе. Правильный подход поможет добиться точного результата и повысить уверенность при работе с системами счисления.