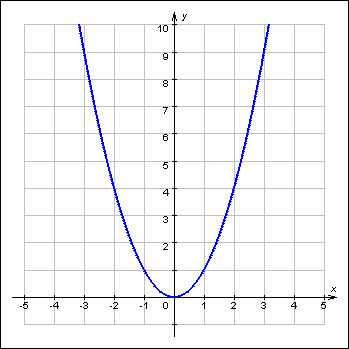
Взгляните на мир алгебры с другой стороны! Все вокруг нас подчиняется математическим законам, и даже хаос можно описать числами. Одной из самых захватывающих тем алгебры в 9 классе является изучение парабол — изящных и грациозных кривых, которые скрывают в себе тайны и секреты численной гармонии.
Ученые и математики с давних времен увлекались изучением парабол, и с каждым открытием все больше внимания уделялось их шаблонам и уравнениям. Ведь именно с помощью алгебры мы можем понять, как и почему парабола принимает такую красивую и определенную форму.
Основная идея этого раздела заключается в том, чтобы рассмотреть шаблон параболы в рамках алгебры 9 класса. Мы постараемся избежать сложных определений и математических формул, сосредоточившись на практической стороне вопроса. Готовы ли вы отправиться в путешествие по игровому полю численной гармонии?
Учебная программа для алгебры в девятом классе

Программа алгебры в девятом классе включает информацию об основных понятиях, таких как уравнения, системы уравнений, функции, графики и многое другое. Учащиеся научатся решать уравнения, работать с координатной плоскостью и строить графики функций. Они также изучат основы алгебры, такие как множества, операции и свойства чисел, полиномы и факторизацию.
| Тема | Основные концепции |
|---|---|
| Уравнения | Решение уравнений, уравнения с одной переменной и системы уравнений |
| Функции | Графики функций, обратные функции, операции с функциями |
| Координатная плоскость | Построение графиков, нахождение координат точек |
| Множества и операции с ними | Пересечение, объединение и разность множеств |
| Полиномы и факторизация | Разложение полиномов на множители, нахождение корней полиномов |
Программа алгебры в девятом классе разработана таким образом, чтобы помочь студентам получить фундаментальные знания и навыки в алгебре, необходимые для более продвинутого изучения математики в будущем. Разделение материала на различные темы позволяет студентам углубляться в каждую концепцию и практиковать свои навыки в решении разнообразных задач.
Практические задачи на кривую второго порядка в 9 классе: примеры и способы решения

Одна из таких задач — определение фокусного расстояния параболы. Фокусное расстояние является важным понятием при работе с параболой и может быть вычислено с использованием особых свойств этой кривой. Мы рассмотрим примеры, где необходимо найти фокусное расстояние и покажем различные способы его определения.
В другой задаче мы будем исследовать траекторию полета тела, брошенного под углом к горизонту с учетом сопротивления воздуха. Для определения этой траектории мы будем использовать уравнения параболы и научимся находить угол броска и высоту максимального подъема.
Еще одной интересной задачей является нахождение точек пересечения параболы с другими кривыми. Мы рассмотрим примеры, где необходимо найти точки пересечения параболы с прямой или окружностью и покажем методы их нахождения.
В этих задачах мы не только познакомимся с параболой, но и разовьем навыки алгебраических операций, графического моделирования и использования различных формул и уравнений. Постепенно углубляясь в решение каждой задачи, вы сможете лучше понять принципы работы параболы и улучшить свои математические навыки.
- Пример 1: Определение фокусного расстояния параболы
- Пример 2: Траектория полета тела
- Пример 3: Точки пересечения параболы с другими кривыми
Данные примеры помогут вам лучше понять параболу и научиться решать задачи, связанные с этой кривой. Постепенно применяйте полученные знания на практике и улучшайте свои навыки в решении сложных задач, где парабола играет важную роль.
Практическое применение параболы в реальной жизни

Одним из основных примеров практического применения параболы является использование ее в фокусировке света. Параболический отражатель или зеркало может сконцентрировать свет в одной точке, что делает его идеальным инструментом для прожекторов, спотов и фар автомобилей. Благодаря свойствам параболы, свет, падающий на зеркало, отражается таким образом, что все световые лучи сходятся в фокусе, образуя яркую точку. Также парабола применяется в антеннах, которые используются в радиосвязи.
Другим полезным примером практического использования параболы является параходостроение. Кормовые гребные винты на судах имеют форму параболы, которая помогает повысить эффективность передачи энергии и улучшает маневренность судна. Параболическая форма обусловлена свойством параболы отражать световые лучи параллельно своей оси, что дает возможность равномерно распределять силу гребли и увеличивать это распределение вдоль кормового гребного винта. Это способствует более эффективному движению судна в воде.
| Область применения | Примеры |
| Оптика и электроника | Фары автомобилей, зеркала в телескопах |
| Архитектура | Спортивные стадионы, крыши зданий |
| Транспорт и навигация | Параходостроение, антенны |
| Развлечения и спорт | Аттракционы, спортивное снаряжение |
Эти примеры демонстрируют, как парабола находит практическое применение в разных сферах нашей жизни, помогая в оптимизации и улучшении различных процессов и конструкций. Узнавая о форме и свойствах параболы, мы можем лучше понять мир вокруг нас и использовать эти знания в практических задачах.
Основные свойства параболы в алгебре: доказательство и объяснение

Фокусное свойство параболы: первым из основных свойств параболы является то, что каждая точка на параболе равноудалена от фокуса и директрисы. Это свойство позволяет геометрически определить форму параболы и ее особенности.
Зеркальное свойство параболы: второе основное свойство параболы заключается в том, что любой луч, падающий на параболу параллельно оси, отражается и проходит через фокус. Это свойство объясняет, почему предметы, находящиеся на определенном расстоянии от фокуса, формируют на экране параболическую проекцию.
Уравнение параболы: третье основное свойство параболы связано с ее уравнением. Уравнение параболы имеет вид y = ax^2 + bx + c, где a, b и c — константы, а x и y — переменные. Доказательство этого свойства позволяет связать уравнение и форму параболы, а также понять, как меняя значения a, b и c, можно изменить форму и положение параболы.
Точка вершины: четвертым основным свойством параболы является то, что вершина параболы всегда находится на оси симметрии и координаты вершины можно найти с помощью формулы x = -b/2a. Доказательство этого свойства позволяет найти вершину параболы и легче анализировать ее график.
Доказательство и объяснение основных свойств параболы помогут ученикам лучше понять ее характеристики и использовать их при решении алгебраических задач.
Практические задания для анализа и построения параболы
Задания включают в себя различные уровни сложности, от простых до более сложных, что позволяет подойти к изучению параболы и ее свойств с разных сторон.
Вы будете изучать основные элементы параболы, такие как вершина, фокус, директриса, их связь с уравнением параболы и графиком. Вы также научитесь строить параболу по заданным параметрам и анализировать ее форму и свойства.
Задания представлены в виде таблицы, где вам будет предложено уравнение параболы или график, и вы должны будете выполнить определенные действия, например, найти вершину, директрису или фокус параболы, или построить график параболы по заданным данным.
| Задание | Описание |
|---|---|
| Задание 1 | Найдите координаты вершины и фокуса параболы, заданной уравнением. |
| Задание 2 | Постройте график параболы по уравнению и определите ее форму и положение в координатной плоскости. |
| Задание 3 | Найдите уравнение директрисы параболы по заданным данным. |
| Задание 4 | Решите систему уравнений, включающую параболу, и определите точки пересечения. |
Эти задания помогут вам закрепить теоретические знания об алгебре и параболах, а также развить навыки анализа и построения данного графика. Решение заданий позволит вам лучше понять и применить принципы алгебры в контексте параболы. Успехов в изучении и анализе параболы!